History of the problem definition
AB testing can be painfully slow. What if we could shift traffic dynamically as we learn which variant performs best?
The name “multi-armed bandit” (MAB) comes from a hypothetical gambling scenario where a player tries to maximize their winnings by choosing which slot machine or “one-armed bandit” to play.
One-armed bandit was the colloquial name for a slot machine in the 1900s in the US, because it has a single lever (“arm”) to operate it.
If each machine has a different true chance of paying out, how much should time and money should the gambler devote to trying “losing” machines before settling on the one they believe to be the best?
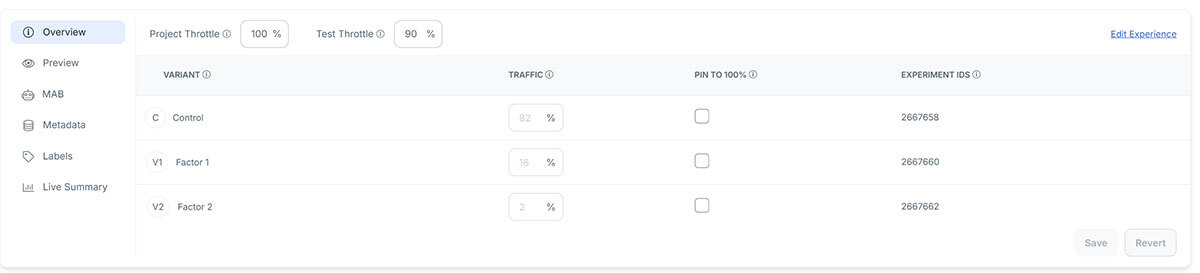
In AB Testing, this corresponds to variants. With a live test where data is continuously rolling in, how much traffic should go to the worse performing variants to give them a chance to recover, before settling on a winner? These two concepts are known as exploration (rolling the dice again) vs exploitation (maximising conversion).
MAB is particularly relevant in short term high-traffic situations, for example a paid campaign driving traffic to the site for one week, or during Black Friday.
Thompson Sampling
We implement Thompson Sampling, which is a Bayesian approach to the problem, with a good balance between exploration and exploitation. Thompson sampling is where you randomly select values from a Bernoulli distribution, compare them, and the larger value wins or is a vote towards that variant being the best.
We sample many times and allocate traffic based on the proportion of times each variant won.
Bernoulli Distribution
To use Thompson sampling, we need to define a Bernoulli distribution, which is a special case of the Binomial distribution. It fits hand in hand with Thompson sampling and is particularly suitable as a model for the data.
The reasons that it is suitable are:
- It is bounded between 0 and 1, which makes perfect sense for conversion rates.
- It is easy to understand, define programmatically, and to update on each iteration.
- It is a natural fit for binary outcomes - i.e. conversion or no conversion.
A Bernoulli distribution is defined by two parameters, Probability of Success (p), which is the current KPI conversion rate for the variant, and Probability of Failure (1 - p), which is the rate of views that did not have conversions, or 1 - conversion rate.
This is a standard statistical model, and a distribution is defined by inputting p and 1 - p. The mean of a Bernoulli distribution is p, or conversion rate. The variance is p * (1 - p).
It is then possible to randomly sample, or draw values, from your Bernoulli distribution. On each iteration, our script defines a new Bernoulli distribution for each variant, based on current conversion rates.
Batch vs Real-time Sampling
Traditional Thompson sampling would operate on the server that delivers the test, i.e. for each user who lands on the page, the server would take one random sample from each variant’s Bernoulli distribution and assign the user to the variant that won.
In our case, we do not do this.
Traffic Allocation Logic
Every 30 minutes, a scheduled job will fetch data for all live tests which have MAB enabled. The script defines a Bernoulli distribution and draws random samples many times. Traffic allocation percentages for each variant are updated in proportion to how often that variant won in the sampling.
Webtrends Optimize Implementation and Smoothing Approach
Thompson Sampling is quite sensitive - for small differences in conversion rate, it gives large swings in traffic allocation percentages. This is problematic, especially at the beginning where there can be large deviations due to small amounts of data and randomness. We don’t want to allocate 99% of traffic to one variant after the experience has been running for just 30 minutes.
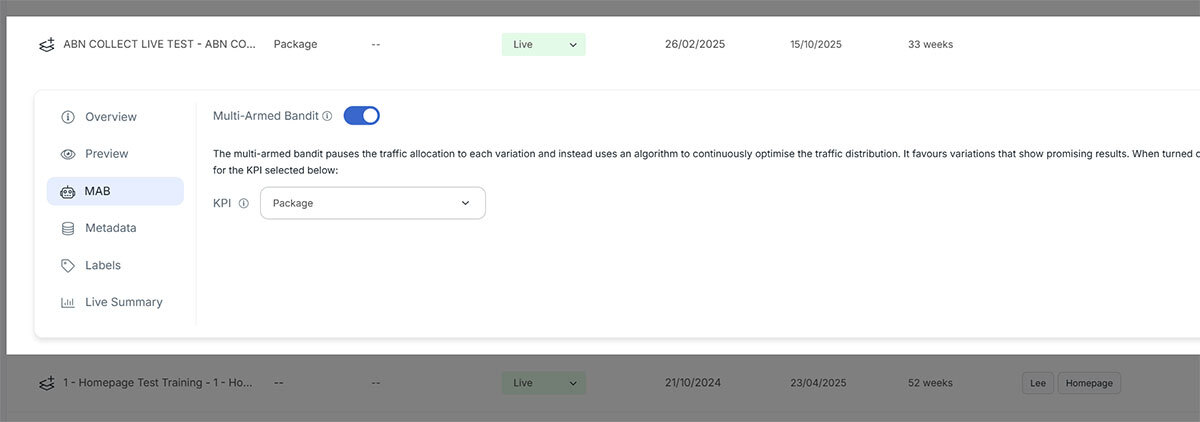
The solution to this problem is to apply custom smoothing, to reduce the rate of change. We apply a custom formula of 0.3 * Thompson Sampling Value + 0.7 * Current Value.
We have built a calculator that can demonstrate this concept, and you are invited to test it out.
The true conversion rates (unknown to the MAB algorithm) can be configured, as well as the number of iterations. You will notice that with close enough conversion rates, the algorithm may change its mind or settle on the wrong winner on some runs, however we believe that Thompson Sampling provides a suitable balance between maximising conversions and making the right decisions.

